Daniel A. Kiefer
Researcher at Institut Langevin
French National Centre for Scientific Research (CNRS)
About me
My research focuses on complex elastodynamic wave phenomena in anisotropic heterostructures, fluid-structure interaction and active media. My work emphasizes exact semi-analytical modeling and specialized numerical solution methods. Together with appropriate signal processing and inverse techniques, this enables sophisticated system and material identification. Application domains include microelectronics, sensors, metalworking, biomedical elastography and more.
Follow me on ResearchGate!
- Wave phenomena, ultrasonics
- Materials: anisotropy, piezoelectricity
- Sensors and microelectronics
Dr.-Ing. in Ultrasonics, 2022
University of Erlangen-Nürnberg, Germany
M.Sc. in Mechatronics, 2016
University of Erlangen-Nürnberg, Germany
Study abroad, 2015
University of British Columbia, Vancouver, Canada
B.Sc. in Mechatronics, 2013
University of Erlangen-Nürnberg, Germany
Experience
- Elastodynamic wave phenomena
- Material monitoring: anisotropic, piezoelectric
- Semi-analytical modeling and specialized numerical solution methods
- Microelectronics, metallurgy, sensing, biomedical elastography
- Zero Group Velocity (ZGV) Lamb waves for material testing and evaluation.
- Teaching: Labwork Waves and Acoustics.
- Non-invasive ultrasonic flow meters based on Lamb waves
- Teaching: Excercise classes CAE of Sensors and Actuators as well as Numerical Simulation of Electro-Mechanical Transducers.
Featured Publications
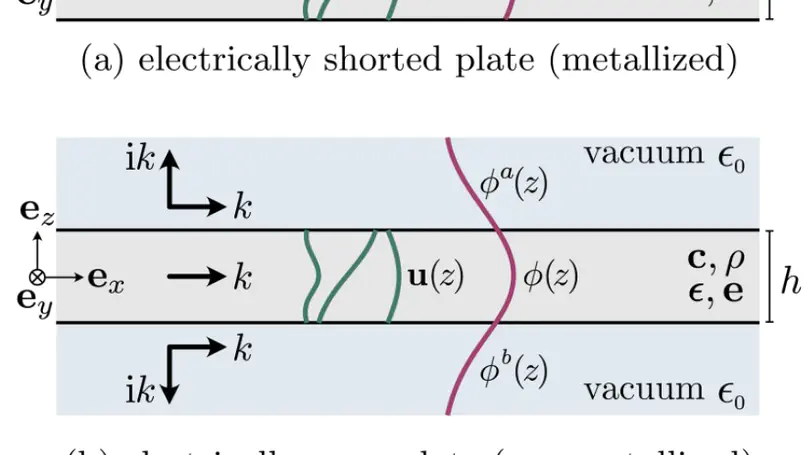
Electroelastic waves in piezoelectric media are widely used in sensing and filtering applications. Despite extensive research, computing the guided wave dispersion remains challenging. This paper presents semi-analytical approaches based on spectral methods to efficiently and reliably compute dispersion curves. We systematically assess the impact of electrical boundary conditions on a 128 ° Y-cut LiNbO 3 wafer, examining open–open, open–shorted, and shorted–shorted surface configurations. Multi-modal dispersion maps obtained from laser-ultrasonic experiments for each boundary condition exhibit excellent agreement with the computational predictions. A straightforward implementation of the spectral collocation method is made available as GEW piezo plate ( https://doi.org/10.5281/zenodo.14205789 ), while the spectral element method is integrated to GEWtool ( http://doi.org/10.5281/zenodo.10114243 ) for multilayered plates. Therewith, we aim to make advanced semi-analytical techniques more accessible to physicists and engineers relying on dispersion analysis.
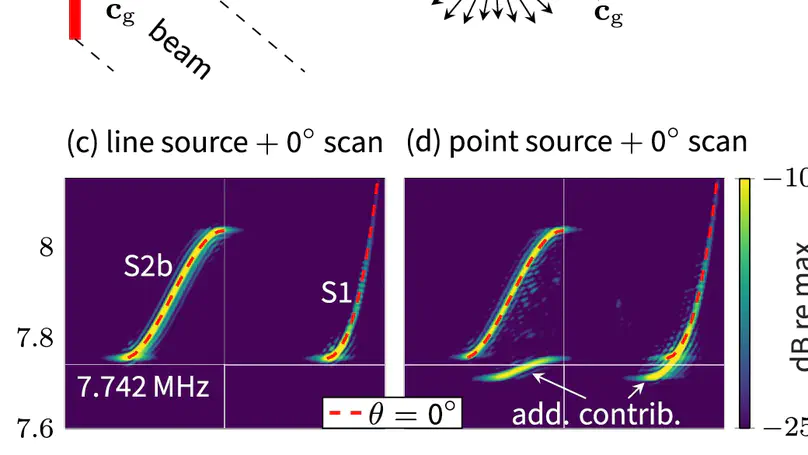
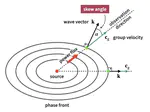
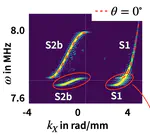
Guided wave dispersion is commonly assessed by Fourier analysis of the field along a line, resulting in frequency-wave-number dispersion curves. In anisotropic plates, a point source can generate multiple dispersion branches pertaining to the same modal surface, which arise due to the angle between the power flux and the wave vector. We show that this phenomenon is very particular near zero-group-velocity points and occurs in all directions independent of the degree of anisotropy. Stationary phase points accurately describe measurements on a monocrystalline silicon plate.

We present a semi-analytical approach to compute quasi-guided elastic wave modes in horizontally layered structures radiating into unbounded fluid or solid media. This problem is of relevance, e.g., for the simulation of guided ultrasound in embedded plate structures or seismic waves in soil layers over an elastic half-space. We employ a semi-analytical formulation to describe the layers, thus discretizing the thickness direction by means of finite elements. For a free layer, this technique leads to a well-known quadratic eigenvalue problem for the mode shapes and corresponding horizontal wavenumbers. Incorporating the coupling conditions to account for the adjacent half-spaces gives rise to additional terms that are nonlinear in the wavenumber. We show that the resulting nonlinear eigenvalue problem can be cast in the form of a multiparameter eigenvalue problem whose solutions represent the wave numbers in the plate and in the half-spaces. The multiparameter eigenvalue problem is solved numerically using recently developed algorithms. Matlab implementations of the proposed methods are publicly available.

To produce sounds, we adjust the tension of our vocal folds to shape their properties and control the pitch. This efficient mechanism offers inspiration for designing reconfigurable materials and adaptable soft robots. However, understanding how flexible structures respond to a significant static strain is not straightforward. This complexity also limits the precision of medical imaging when applied to tensioned organs like muscles, tendons, ligaments and blood vessels among others. In this article, we experimentally and theoretically explore the dynamics of a soft strip subject to a substantial static extension, up to 180%. Our observations reveal a few intriguing effects, such as the resilience of certain vibrational modes to a static deformation. These observations are supported by a model based on the incremental displacement theory. This has promising practical implications for characterizing soft materials but also for scenarios where external actions can be used to tune properties.

Elastic waves in anisotropic media can exhibit a power flux that is not collinear with the wave vector. This has notable consequences for waves guided in a plate. Through laser-ultrasonic experiments, we evidence remarkable phenomena due to slow waves in a single-crystal silicon wafer. Waves exhibiting power flux orthogonal to their wave vector are identified. A pulsed line source that excites these waves reveals a wave packet radiated parallel to the line. Furthermore, there exist precisely eight plane waves with zero power flux. These so-called zero–group-velocity modes are oriented along the crystal’s principal axes. Time acts as a filter in the wave-vector domain that selects these modes. Thus, a point source leads to beating resonance patterns with moving nodal curves on the surface of the infinite plate. We observe this pattern as it emerges naturally after a pulsed excitation.
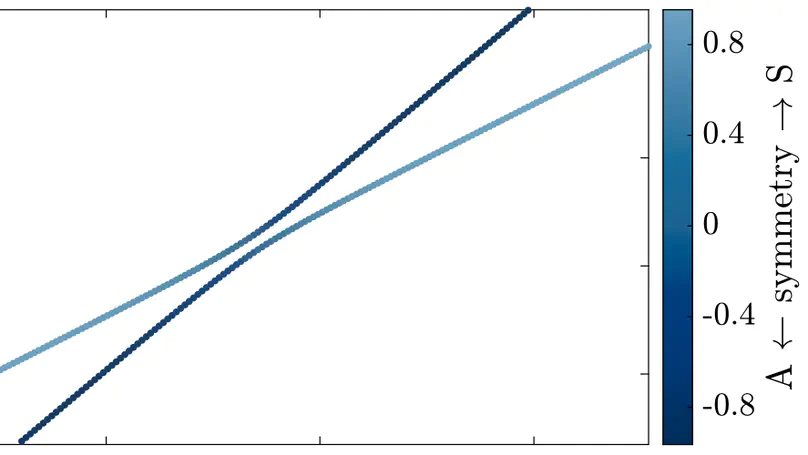
The dispersion curves of (elastic) waveguides frequently exhibit crossings and osculations (also known as veering, repulsion, or avoided crossing). Osculations are regions in the dispersion diagram where curves approach each other arbitrarily closely without ever crossing before veering apart. In semi-analytical (undamped) waveguide models, dispersion curves are obtained as solutions to discretized parameterized Hermitian eigenvalue problems. In the mathematical literature, it is known that such eigencurves can exhibit crossing points only if the corresponding matrix flow (parameter-dependent matrix) is uniformly decomposable. We discuss the implications for the solution of the waveguide problem. In particular, we make use of a simple algorithm recently suggested in the literature for decomposing matrix flows. We also employ a method for mode tracing based on approximating the eigenvalue problem for individual modes by an ordinary differential equation that can be solved by standard procedures.

Dispersion curves of elastic waveguides exhibit points where the group velocity vanishes while the wavenumber remains finite. These are the so-called zero-group-velocity (ZGV) points. As the elastodynamic energy at these points remains confined close to the source, they are of practical interest for nondestructive testing and quantitative characterization of structures. These applications rely on the correct prediction of the ZGV points. In this contribution, we first model the ZGV resonances in anisotropic plates based on the appearance of an additional modal solution. The resulting governing equation is interpreted as a two-parameter eigenvalue problem. Subsequently, we present three complementary numerical procedures capable of computing ZGV points in arbitrary nondissipative elastic waveguides in the conventional sense that their axial power flux vanishes. The first method is globally convergent and guarantees to find all ZGV points but can only be used for small problems. The second procedure is a very fast, generally-applicable, Newton-type iteration that is locally convergent and requires initial guesses. The third method combines both kinds of approaches and yields a procedure that is applicable to large problems, does not require initial guesses and is likely to find all ZGV points. The algorithms are implemented in GEW ZGV computation (doi: 10.5281/zenodo.7537442).
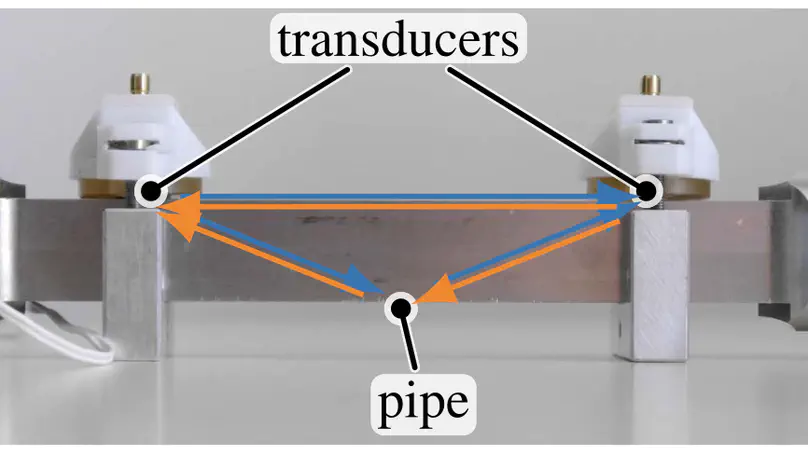
Transit-time flow meters need to compensate for cross-sensitivity to temperature. We show that Lamb wave-based setups are less affected by temperature. An optimality criterion is derived that allows to tune the meter into a zero local sensitivity to temperature. For this end, the flow-induced change in ultrasonic transit time is revisited first. While wetted piston transducer meters are directly sensitive to the change in propagation speed, the change in time of flight of Lamb wave-based systems is due to the beam displacement. Second, the effect of temperature is incorporated analytically. It is found that the temperature-dependent radiation angle of Lamb waves is able to compensate for changes in the speed of sound, leading to an (almost) unaffected overall time of flight. This effect is achievable with any fluid and in a wide temperature range. As an example, we discuss a water meter in the range from 0°C to 100°C. The model is validated against temperature and flow rate-dependent measurements obtained on a prototype. The measured data fits well to the developed model and confirms the reduced cross-sensitivity to temperature. Although an in-line meter is considered here, the results extend to clamp-on devices.
Recent & Upcoming Talks
Contact
- daniel.kiefer@espci.fr
-
1 rue Jussieu
75005 Paris