Waves in piezoelectric plates: semi-analytical modeling and laser-ultrasound experiments

Abstract

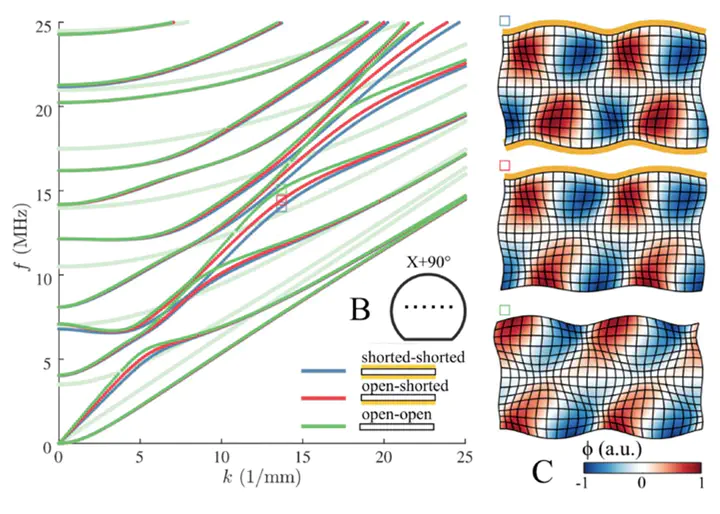
Piezoelectric layered materials are widely used in electronics for sensing and filtering applications. Waves propagating therein consists of a coupled electroelastic field. Conventional computational methods rely on root-searching of the characteristic equations, which is known to be slow and miss solutions. To resolve these issues, semi-analytical methods that discretize the resonant field have been developed extensively, in particular for purely elastic waveguides. In this contribution we present a semi-analytical approach based on spectral methods to compute electroelastic guided waves in plates. Electrically shorted (metallized surfaces) and open (non-metallized surfaces) plates can be considered. The effect of the electrical boundary conditions is analyzed and we find that the dispersion spectra are affected considerably. A monocrystalline 128° Y-cut Lithium Niobate (LiNbO3) wafer serves as a relatively simple test specimen. Our computations are in very good agreement with laser-ultrasonic measurements performed on electrically open-open, open-shorted and shorted-shorted wafers.

Daniel A. Kiefer

Researcher at Institut Langevin

Research in guided elastodynamic waves, fluid-structure interaction, simulation and signal processing for ultrasonic sensors and nondestructive testing.