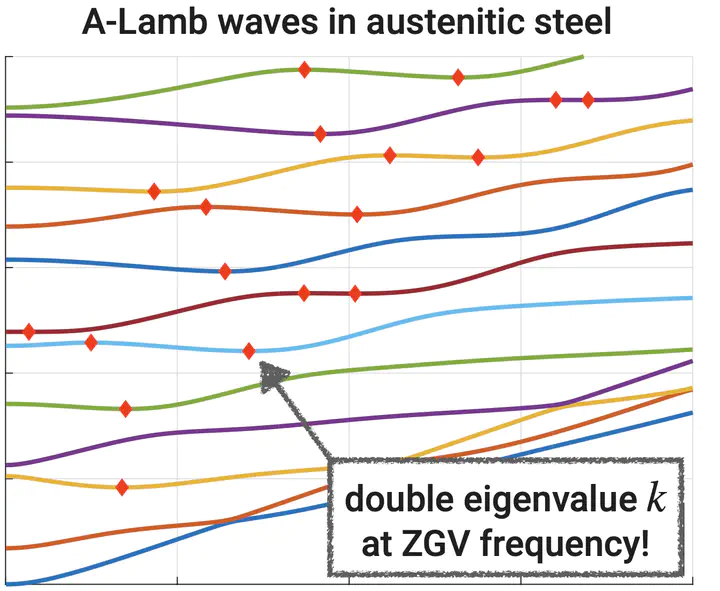
Locating Zero-Group-Velocity Points in Elastic Waveguides

Abstract

Zero-Group-Velocity (ZGV) resonances are a powerful tool for nondestructive testing of thin-walled components. The latter act as mechanical waveguides whose dispersion curves exhibit isolated frequency-wavenumber points where the group velocity of the wave vanishes. A strong resonance is usually observed at these so-called ZGV points, making them easily measurable in experiments. It is very valuable for the mentioned applications to be able to predict these resonances. For this purpose, we developed reliable and fast methods to compute ZGV points in anisotropic and transversely-inhomogeneous waveguides of potentially generic shape[1]. Multiple ZGV points on a single branch can exist in this case, making a simple search infeasible. The general task of computing ZGV points is remarkably difficult because two eigen-parameters, namely the frequency and the wavenumber, need to be computed simultaneously. For this purpose, the ZGV resonance is modeled through the appearance of an exceptional mode as was previously done by Tassoulas and Akylas[2]. We then proceed by interpreting the resulting system as a two-parameter eigenvalue problem that we denote as the ZGV problem. Solving it leads to a globally convergent computational procedure capable of locating all ZGV points without initial guesses. As the associated computational cost is very high, an extremely fast yet general Newton-type iteration has also been developed. Its regions of convergence are depicted in Fig. 1. This method can be employed to refine initial approximations obtained using a reduced and regularized version of the ZGV problem, leading to a substantially faster method which does not require initial guesses.

Daniel A. Kiefer

Researcher at Institut Langevin

Research in guided elastodynamic waves, fluid-structure interaction, simulation and signal processing for ultrasonic sensors and nondestructive testing.